【五ツ木・駸々堂 第3回模試】平均点と標準偏差から読み解く近年の傾向
はじめに
五ツ木・駸々堂模試の第3回は、年間でも中盤に差し掛かる重要なタイミングで実施されます。
この模試をどう位置づけるかは、受験生の学習戦略に直結します。
今回は2019年度〜2023年度の第3回模試における平均点と標準偏差を分析し、
「年ごとの傾向」および「教科ごとの特徴」を明らかにします。
各年度の平均点・標準偏差(第3回模試)
| 年度 | 国語 | 算数 | 理科 | 社会 | 4科A |
|---|---|---|---|---|---|
| 2023 | 38.78/16.88 | 44.70/22.62 | 45.38/17.43 | 47.91/17.02 | 179.37/63.10 |
| 2022 | 52.28/17.62 | 40.66/22.13 | 40.27/15.38 | 46.78/16.87 | 181.87/62.52 |
| 2021 | 41.88/17.60 | 48.54/22.83 | 46.96/17.68 | 45.32/17.26 | 184.53/64.91 |
| 2020 | 49.24/19.48 | 40.79/23.60 | 45.70/17.71 | 43.44/17.70 | 181.14/68.12 |
| 2019 | 45.00/18.40 | 33.00/19.80 | 32.00/15.50 | 40.00/17.70 | 152.00/61.70 |
※左:平均点、右:標準偏差
模試の成績表に「平均点」や「偏差値」と並んでよく記載されているのが「標準偏差」です。
これは、受験者の得点がどれだけバラついているかを示す数値です。
標準偏差が示すこと
- 標準偏差が大きい
→ 点数に差がある。できる子とできない子の実力差が表れた。 - 標準偏差が小さい
→ 点数に差がない。多くの受験者が同じくらいの得点だった。
たとえば…
- 国語:標準偏差16.8 → みんなだいたい同じ点数
- 算数:標準偏差22.6 → 点数に差が出やすく、勝負が分かれた
このように、どの教科で差がついたかを見極める際に、標準偏差はとても有効です。
標準偏差の計算式(参考)
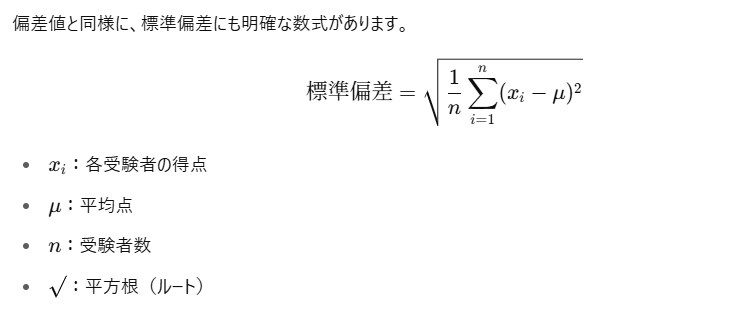
つまり、「各人の得点が平均からどれだけ離れているか」を集計し、その平均的なズレを示したものです。
算数に見られる最大のばらつき
この5年のデータを比較すると、算数の標準偏差が他教科より一貫して大きいことが明らかです。
- 他教科が概ね16〜18台で安定しているのに対し、
- 算数のみが毎年20〜23台という大きなばらつき
これは、算数が最も実力差が反映されやすく、差がつきやすい教科であることを示しています。
第3回に特有の傾向はあるか?
結論から言うと、第3回に明確な傾向はありません。
- 平均点・標準偏差ともに、年ごとのバラつきが非常に大きい
- 特に算数は30点台〜40点台後半まで幅広く、年度によって難易度が大きく異なる
したがって、「第3回だから易しい」「第3回は例年難しい」といった固定的な見方は避けるべきです。
それでも見えてくるもの
唯一共通して言えるのは、算数が最も得点差を生む教科であること。
- できる生徒は高得点を叩き出し、苦手な生徒は大きく崩れる
- そのため、合否に直結する要素としての重要性が高い
教育現場からの補足コメント(有水の見解)
「できる子が取れて、できない子が取れない」──
この構図が最もはっきり出るのが、五ツ木・駸々堂の算数です。
逆にいえば、算数の苦手を克服できれば、偏差値・順位ともに一気に上がる可能性があるということでもあります。
第3回模試は、現状の立ち位置を把握しつつ、夏〜秋の学習の質と量を見直す材料として活用するのが最善です。
有水の指導:本番を意識した類題トレーニング
模試の分析や標準偏差の読み取りは、あくまで「現状の理解」のためのものです。
実際の受験で結果を出すためには、それをふまえた具体的な対策が必要になります。
私の指導では、こうした模試や過去問の出題傾向をふまえて、
- 各生徒のレベルに合わせた「過去問類似問題」を作成
- 実際の試験形式に近い形で取り組ませる
- 解き方だけでなく、解答の過程・選択の根拠・図示や条件整理の力も鍛える
といった形で、本番での得点力を高める指導を行っています。









